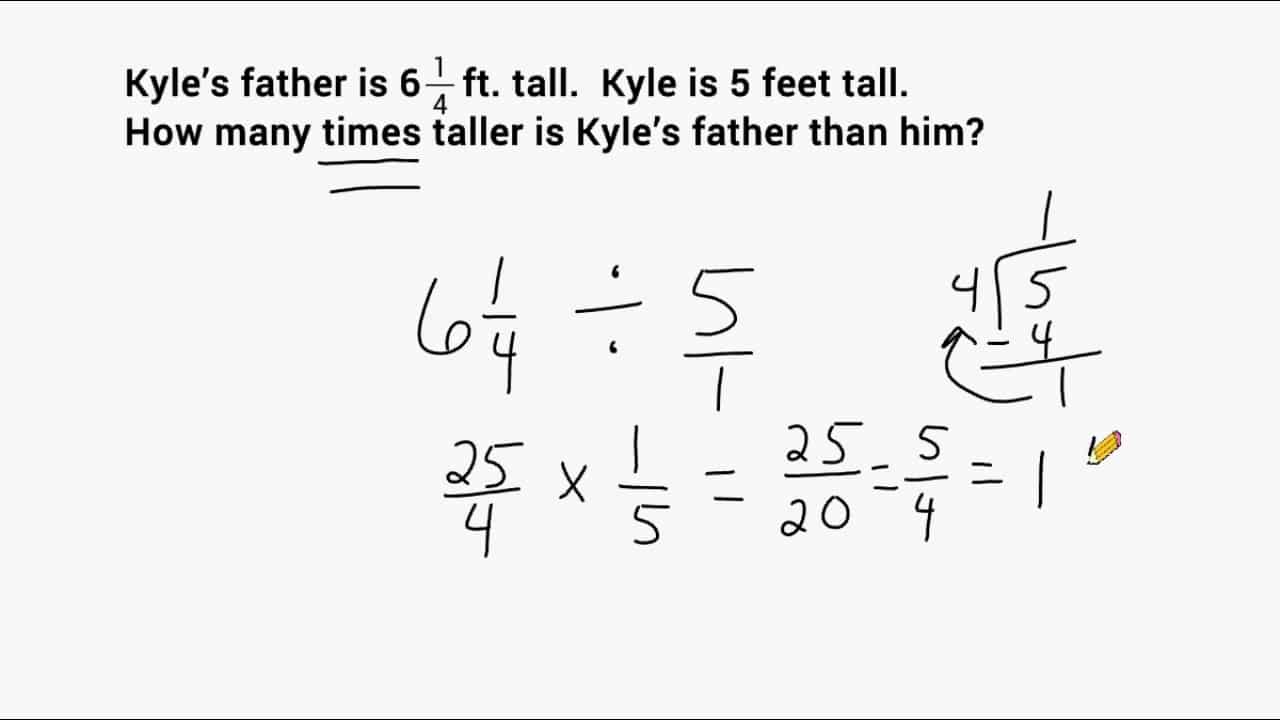Fractions play a fundamental role in mathematics, representing parts of a whole and enabling us to express numerical quantities with precision. While fractions may seem challenging at first, it is crucial to learn how to divide fractions with whole numbers for mathematical problem-solving skills.
Fortunately, this guide delves into the intricacies of dividing fractions with whole numbers, empowering you with the knowledge and techniques to tackle these problems with confidence.
Table of contents
- Explaining Fractional Division
- What are the Strategies for Tackling Word Problems?
- How does the concept of dividing fractions with whole numbers relate to other mathematical operations?
- What are some common misconceptions about dividing fractions with whole numbers?
- How can students understand the division of fractions with whole numbers?
- What role does technology play in learning about dividing fractions with whole numbers?
- How can teachers assess students’ understanding of dividing fractions with whole numbers?
- What are some future directions in research and teaching related to dividing fractions with whole numbers?
- FAQs
- Conclusion
- References
- Recommendations
Explaining Fractional Division
1. Conceptualizing the Division Process
Dividing a fraction by a whole number can be visualized as distributing the whole number into equal portions, each representing a fraction of the original whole. This concept helps break down the problem into more manageable segments.
2. Converting Whole Numbers to Fractions
Since division involves two fractions, it is often necessary to convert the whole number into an equivalent fraction with a denominator of 1. This can be done by adding the whole number to the denominator of a fraction with a numerator of 1.
3. The Flip-and-Multiply Technique
The most common method for dividing fractions with whole numbers involves a simple yet effective technique known as “flip and multiply.” This method involves flipping the whole number fraction (converting the whole number to a fraction with a denominator of 1) and then multiplying the two fractions.
4. Simplifying the Resulting Fraction
After multiplying the two fractions, the resulting product may be in the form of a complex fraction. In such cases, it is essential to simplify the fraction by finding the greatest common factor (GCD) of the numerator and denominator and dividing both by the GCD.
You can also read: How to Find Average Rate of Change: Calculus Concept Simplified
What are the Strategies for Tackling Word Problems?
1. Identifying the Key Information:
When encountering word problems involving the division of fractions, it is crucial to carefully read the problem and identify the key pieces of information. This includes the quantities involved, the relationship between them, and the mathematical operation to be performed.
2. Translating the Problem into Mathematical Language:
Once the key information has been identified, the next step is to translate the problem into mathematical language. This involves assigning variables to unknown quantities and expressing the relationships between them using appropriate mathematical symbols.
3. Applying the Division Technique:
With the problem translated into mathematical notation, the division technique can be applied to solve for the unknown quantity. Remember to convert whole numbers to fractions and simplify the resulting fraction.
4. Interpreting the Solution:
Once the mathematical solution has been obtained, it is essential to interpret it in the context of the original word problem. This involves ensuring that the solution makes sense and corresponds to the real-world scenario presented in the problem.
How does the concept of dividing fractions with whole numbers relate to other mathematical operations?
Dividing fractions with whole numbers is closely related to the concept of multiplying fractions. In fact, dividing a fraction by a whole number can be seen as multiplying the fraction by the reciprocal of the whole number. This understanding helps connect different mathematical operations and demonstrates the underlying principles of fractional arithmetic.
Read also: How Many Miles is a 10K: Accurate Distance Insights for Running Enthusiasts
What are some common misconceptions about dividing fractions with whole numbers?
A common misconception is that dividing a fraction by a whole number is the same as subtracting the whole number from the fraction. However, this is incorrect, as subtraction involves removing a part of a whole, while division involves distributing a whole into equal parts.
Another misconception is that dividing a fraction by a whole number always results in a smaller fraction. This is not always the case, as the result can be a larger fraction or even a whole number depending on the values involved.
How can students understand the division of fractions with whole numbers?
Encouraging students to engage in hands-on activities and visual representations can help deepen their understanding of dividing fractions with whole numbers. Using fraction manipulatives, such as fraction circles or fraction bars, can make the concept more concrete and relatable to real-world scenarios.
Additionally, incorporating real-world examples and problem-solving scenarios can motivate students and help them appreciate the practical applications of this mathematical skill.
What role does technology play in learning about dividing fractions with whole numbers?
Technology has revolutionized the way mathematics is taught and learned, providing interactive tools and engaging platforms that make abstract concepts more accessible. Numerous online resources, educational apps, and interactive simulations can be utilized to enhance students’ understanding of dividing fractions with whole numbers.
These tools can provide personalized instruction, offer immediate feedback, and adapt to individual learning styles, making the learning process more effective and enjoyable.
How can teachers assess students’ understanding of dividing fractions with whole numbers?
A variety of assessment methods can be employed to evaluate students’ comprehension of dividing fractions with whole numbers. Traditional pen-and-paper tests, while still valuable, can be supplemented with more creative and engaging assessments.
Consider incorporating real-world problem-solving scenarios, group projects, and presentations to assess students’ ability to apply their knowledge in different contexts.
See also: How Long Did It Take Noah to Build the Ark: Historic Construction Feat Explored
Researchers continue to explore innovative ways to enhance the teaching and learning of dividing fractions with whole numbers. One area of focus is developing more effective instructional strategies that incorporate technology, engage diverse learning styles, and promote deeper conceptual understanding.
Additionally, research is exploring the integration of dividing fractions with whole numbers into broader mathematical concepts and real-world applications, fostering a more interconnected and meaningful learning experience.
FAQs
Converting whole numbers to fractions ensures that both quantities involved in the division are expressed in the same form, allowing for a consistent and accurate application of the division technique.
Simplifying the resulting fraction helps to express the answer in its most concise and meaningful form. It eliminates unnecessary common factors, making the fraction easier to understand and interpret.
When tackling word problems involving the division of fractions, it is essential to follow a structured approach:
Carefully read the problem and identify the key information.
Translate the problem into mathematical language using variables and appropriate symbols.
Apply the division technique to solve for the unknown quantity.
Interpret the solution in the context of the original word problem.
While the flip-and-multiply technique is the most common method, there are alternative approaches, such as using long division or multiplying both fractions by a common denominator.
Numerous online resources, practice problems, and interactive tutorials can provide valuable practice opportunities for mastering the division of fractions with whole numbers.
Conclusion
Dividing fractions with whole numbers is an essential skill in mathematics, enabling individuals to tackle a wide range of problems and develop their problem-solving abilities. By understanding the conceptual framework, employing effective techniques, and practicing with a variety of problems, individuals can overcome any initial challenges and gain confidence in their mathematical proficiency.
References
- study.com – How to Divide Fractions | Formula, Steps & Examples
- indeed.com – How To Divide Fractions: 2 Easy Methods (With Examples)