When you multiply a whole number with a fraction, it is first written in fraction form and then multiplied by the provided fraction according to the multiplication of fractions rules.
It’s important to keep in mind that the given fractions may be either an improper or proper fraction when multiplying them by whole numbers.
With several examples, let’s study more about multiplying fractions with whole numbers.
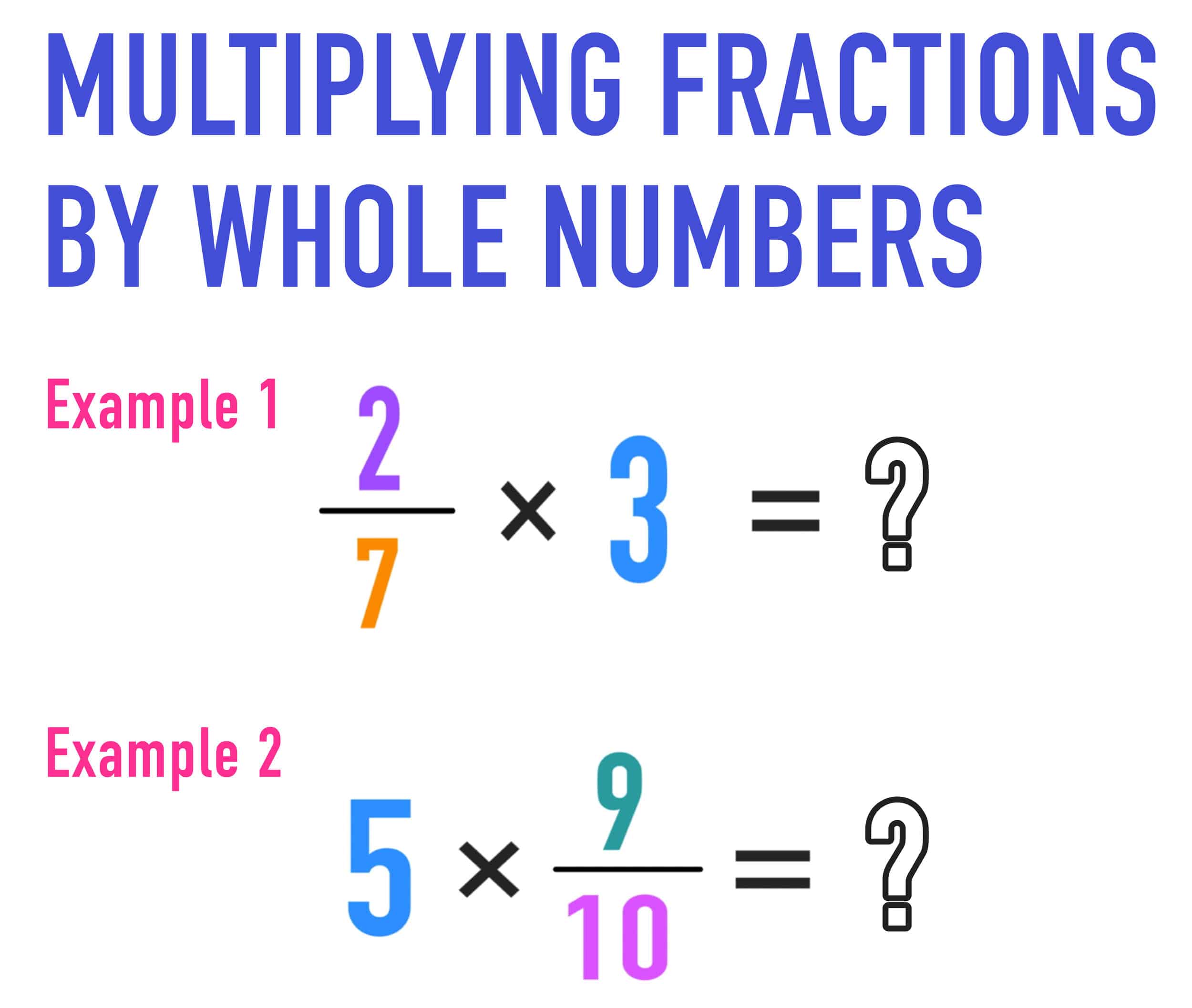
Table of contents
What is Multiplying Fractions With Whole Numbers?
Like repeated addition, when the fraction is added the same number of times as the whole number, multiplying fractions by whole numbers is similar. In order to multiply a fraction, we multiply the numerators first, followed by the denominators, and then we express the resulting fraction to its lowest terms.
Nevertheless, we express the whole number in the form of a fraction by writing 1 as its denominator when we need to multiply fractions by whole numbers.
We can multiply it using the same methods after this step. For instance, (a × c) / (b × d) is the result of multiplying the fraction a/b × c/d. When multiplying fractions by whole numbers, this rule also applies.
See also: How to Find the Domain of a Function: A Guide for Math Enthusiasts
How to Multiply Fractions With Whole Numbers?
The idea of multiplying fractions with whole numbers is simple. All we have to do is write the exact whole number as the numerator and 1 as the denominator to turn the whole number into a fraction. After that, the specified fraction is multiplied. The outcome of multiplying these should be either a mixed fraction or a proper fraction. We can then convert the result to a mixed fraction if it is in an improper fraction.
Let’s use an example to better understand the steps.
Example 1: Multiply 2/7 × 3
Solution: Here, 2/7 is the fraction and 3 is the whole number.
- Step 1: Convert the whole number to a fraction by writing 1 as the denominator. This means 3 is written as 3/1
- Step 2: Multiply the numerators. Here, 2 × 3 = 6
- Step 3: Multiply the denominators. Here, 7 × 1 = 7
- Step 4: Simplify and reduce the product, if needed. If the result is an improper fraction, we convert it to a mixed fraction. So, the product is 6/7.
Let us look at another example to understand this better.
Example 2: Multiply 3 × 7/10.
Solution: Here, 3 is the whole number and 7/10 is the proper fraction.
- Step 1: We convert the whole number 3 into a fraction by writing 1 as the denominator. This means 3 is written as 3/1.
- Step 2: Multiply the numerators of both the fractions. 3/1 × 7/10 = 3 × 7 = 21.
- Step 3: Multiply the denominators of both the fractions. 3/1 × 7/10 = 1 × 10 = 10.
- Step 4: Simplify the fractions. 3/1 × 7/10 = 21/10. We can simplify this further. This means, 21/10 = 2
.
Therefore, 5 × 3/10 = 3/2 = 1 .
See also: How Many Sides Does a Pentagon Have? Geometric Basics
How to Multiply Mixed Fractions with Whole Numbers?
We must first convert a mixed fraction into an improper fraction before multiplying it by the whole number in order to multiply mixed fractions with whole numbers.
Example: Multiply 3 with 20.
Solution: Let us see how to multiply the given mixed fraction with a whole number.
- Step 1: First let us convert the mixed fraction to an improper fraction. This means 3
= 13/4.
- Step 2: Then, convert the whole number 20 into a fraction. This means 20 = 20/1. This makes it 13/4 × 20/1
- Step 3: Multiply the numerators of both the fractions. 13 × 20 = 260. Multiply the denominators of both the fractions. This means 4 × 1 = 4.
- Step 4: Simplify and reduce the fraction, that is, 260/4 = (260 ÷ 4) / (4 ÷ 4) = 65/1. Therefore, 3
× 20 = 65.
See also: How to Find Coterminal Angles | Definition and Application
Examples on Multiplying Fractions With Whole Numbers
- Example 1: Multiply the fraction with the whole number: 1/4 × 12
Solution:
Let us multiply the fraction with the whole number,
1/4 × 12 = 1/4 × 12/1 = (1 × 12) / (4 × 1) = 12/4 = 3.
Therefore, 1/4 × 12 = 3
- Example 2: Find the product after multiplying the fraction with the whole number: 4/5 × 5.
Solution:
For multiplying fractions with whole numbers, we need to change the whole number to a fraction by writing 1 as its denominator.
4/5 × 5 = 4/5 × 5/1 = (4 × 5) / (5 × 1) = 20/5 = 4.
Therefore, 3/4 × 4 = 3
- Example 3: Find the product of the whole number 5 and the mixed fraction 2
Solution:
Let us first convert the mixed fraction to a proper fraction.
2 = [(7 × 2) + 4] / 7 = 18/7
Let us convert the whole number to fraction,
5 = 5/1
Now let us multiply the fraction with the whole number,
5/1 × 18/7 = (5 × 18) / (1 × 7) = 90/7
Once the result is obtained we convert this into a mixed fraction.
90/7 = 12 .
See also: How to be Good at Math
FAQs
1: Convert the mixed number into an improper fraction.
2: Rewrite the whole number as a fraction with the denominator 1.
3: Multiply two fractions by multiplying the numerators and denominators separately.
4: Convert it into simplified form if required.
Conclusion
Multiplying fractions with whole numbers might seem daunting at first, but with practice and a clear understanding of the steps involved, you’ll become a pro in no time. Happy calculating!
References
- Cuemath.com – Multiplying Fractions with Whole Numbers
- Study.com – How to Multiply Fractions with Whole Numbers
Recommendations
- How Many Weeks in a Month: A Deep Dive into Calendar Math
- What Do You Study in College (Basic Courses)
- How Tall Is 48 Inches In Feet: Conversion Insights
- How Many Milliseconds Are in a Second: Understanding Time Conversions
- How Many Days in a Year: Exploring Calendar Variations
- How Many Yards In A Mile: Understanding Length Units