Keyword: coterminal angles definition
Angles are fundamental concepts in geometry and trigonometry, and understanding how to work with them is crucial for various applications in mathematics and science. A critical aspect of angles that often comes up in these fields is coterminal angles. In this article, we will explore coterminal angles, how to find them, and their practical applications.
Understanding Coterminal Angles
Coterminal angles are angles that share the same initial and terminal sides. In simpler terms, coterminal angles have the same position in the standard work on the coordinate plane. The primary difference between coterminal angles lies in the number of complete rotations they make. When an angle is measured in degrees, it’s common to work from 0 to 360 degrees. However, angles beyond this range can be considered coterminal if they end up in the same position.
For instance, consider the angle of 45 degrees. If you add 360 degrees to it, you get 405 degrees. Both 45 and 405 degrees are coterminal angles because they represent the same standard position.
Finding Coterminal Angles
To find coterminal angles, add or subtract multiples of 360 degrees to the given angle until you reach a rise within the 0-360 degree range. This process can be described as follows:
- Start with the given angle that you want to find coterminal tips.
- If the angle is positive, subtract 360 degrees from it until it falls within the 0-360 degree range. Keep doing this until you obtain a grade that meets the criteria.
- If the angle is negative, add 360 degrees until it falls within the 0-360 degree range. Continue adding 360 degrees until you get an angle that satisfies the condition.
Let’s look at a couple of examples to illustrate this process:
Example 1: Finding Coterminal Angles for 480 degrees
Given angle: 480 degrees
To find coterminal angles, subtract 360 degrees: 480 degrees – 360 degrees = 120 degrees.
The coterminal angle for 480 degrees is 120 degrees.
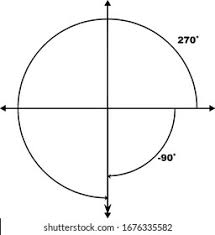
Example 2: Finding Coterminal Angles for -90 degrees
Given angle: -90 degrees
To find coterminal angles, add 360 degrees: -90 degrees + 360 degrees = 270 degrees.
The coterminal angle for -90 degrees is 270 degrees.
Practical Applications of Coterminal Angles
Coterminal angles are not just mathematical abstractions; they have critical practical applications in various fields, particularly trigonometry and engineering. Here are a few scenarios where coterminal angles come into play:
- Navigation: Coterminal angles are used in navigation and map reading to calculate the direction from one point to another. Sailors, pilots, and hikers often use coterminal angles to determine the most efficient route.
- Electrical Engineering: In electrical engineering, coterminal angles are used to calculate phase differences in alternating current (AC) circuits. This information is crucial for understanding the behavior of AC signals and designing electrical systems.
- Robotics and Mechanics: Coterminal angles are essential for controlling robotic arms and mechanisms. Engineers use coterminal angles to ensure that mechanical movements are precise and accurate.
- Trigonometry: Coterminal angles play a significant role in trigonometric functions and identities, simplifying calculations and problem-solving in various mathematical and scientific applications.
Frequently Asked Questions
1.What are coterminal angles? Coterminal angles have the same initial and terminal sides in the standard position on the coordinate plane.
2. How do you find coterminal angles? To find coterminal angles, add or subtract multiples of 360 degrees to an angle until it falls within the 0-360 degree range.
3. Why are coterminal angles important in trigonometry? Coterminal angles are crucial for simplifying trigonometric calculations and solving problems involving angles and functions.
4. Can negative angles have coterminal angles? Yes, negative angles can have coterminal angles. Adding 360 degrees repeatedly to a negative angle will yield coterminal angles within the 0-360 degree range.
5. In what practical applications are coterminal angles used? Coterminal angles find applications in navigation, electrical engineering, robotics, mechanics, and trigonometry, where they simplify calculations and aid in problem-solving.
Conclusion
Coterminal angles share the same initial and terminal sides and are often used to simplify calculations and solve problems in mathematics, engineering, and other scientific fields. Understanding how to find coterminal angles is a fundamental skill that can be applied to many real-world situations, making it an essential concept for anyone working with angles and trigonometry.
References
- study.com: Coterminal angles.
- wikihow.com: Coterminal angles.